Derivation of Parametric Equations of a Line with Example YouTube

The collection of points that we get by letting t t be all possible values is the graph of the parametric equations and is called the parametric curve. To help visualize just what a parametric curve is pretend that we have a big tank of water that is in constant motion and we drop a ping pong ball into the tank.

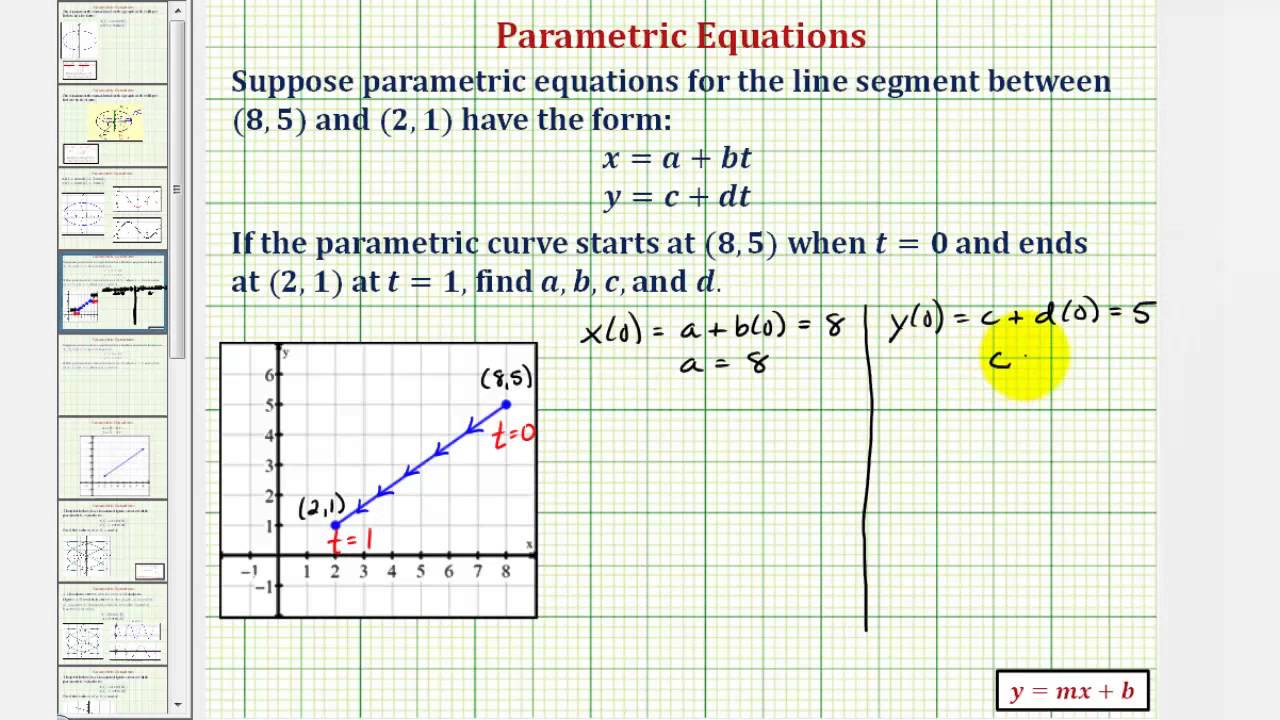
Find the Parametric Equations for a Line Segment Given an Orientation

Learning Objectives. Plot a curve described by parametric equations. Convert the parametric equations of a curve into the form \(y=f(x)\). Recognize the parametric equations of basic curves, such as a line and a circle.

Find Parametric Equations and Symmetric Equations for the Line

Answer The parametric form of the equation of a line passing through the point ( 𝑥, 𝑦) and parallel to the direction vector ( 𝑎, 𝑏) is 𝑥 = 𝑥 + 𝑎 𝑘, 𝑦 = 𝑦 + 𝑏 𝑘. We are given that our line has a direction vector ⃑ 𝑢 = ( 2, − 5) and passes through the point 𝑁 ( 3, 4), so we have ( 𝑥, 𝑦) = ( 3, 4), ( 𝑎, 𝑏) = ( 2, − 5).

parametric equation of line part one vector YouTube

To rewrite the parametric equation in the form of a rectangular equation, we are trying to develop a relationship between x and y whereas eliminating t. For example, if we want to write a parametric equation of the line that passes through point A (q, r, s) and is parallel to the direction vector v . The equation of the line is.

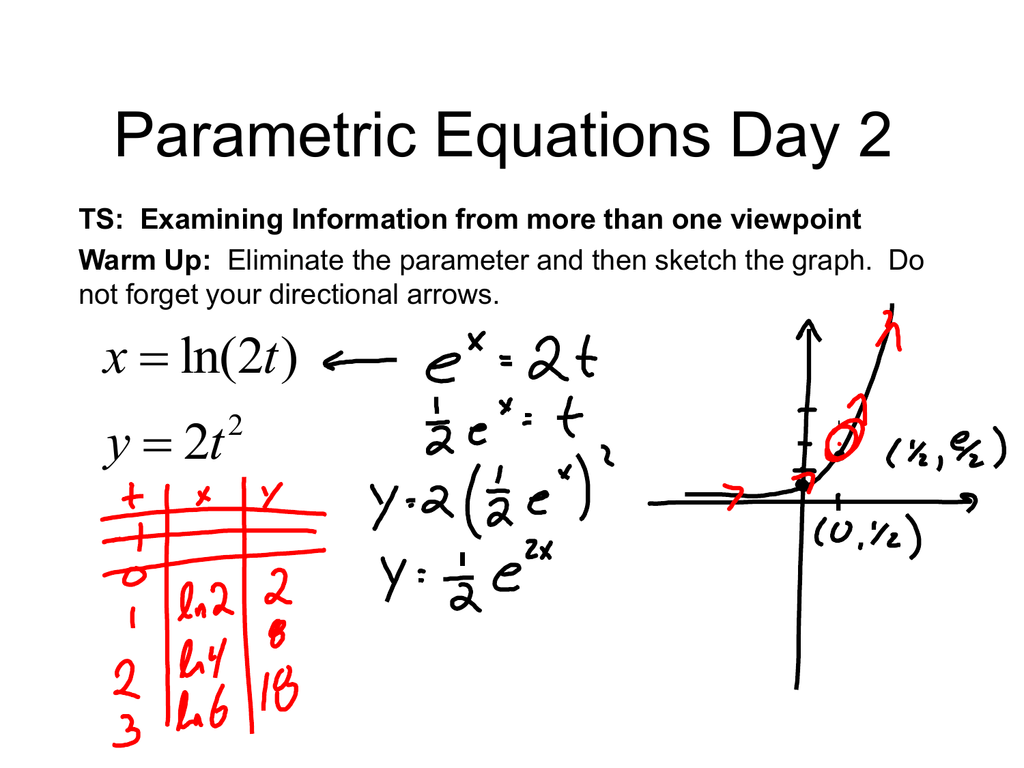
Parametric Equations

In mathematics, a parametric equation defines a group of quantities as functions of one or more independent variables called parameters. [1] Parametric equations are commonly used to express the coordinates of the points that make up a geometric object such as a curve or surface, called a parametric curve and parametric surface, respectively.

Lesson Equation of a Straight Line Parametric Form Nagwa

Consider the line given by (4.6.2) (4.6.2). You can solve for the parameter t t to write. t = x − 1 t = y−2 2 t = z t = x − 1 t = y − 2 2 t = z. Therefore, x − 1 = y − 2 2 = z x − 1 = y − 2 2 = z. This is the symmetric form of the line. In the following example, we look at how to take the equation of a line from symmetric form.

PPT The parametric equations of a line PowerPoint Presentation, free

I know that to get the parametric equations of a line, you need a vector parallel to that line and a point on the line. So question 1) seems pretty straightforward. The vector PQ→ =< 2, −1, 3 > P Q → =< 2, − 1, 3 > is obviously parallel to the line since it includes the line. So the answer is x = 1 + 2t x = 1 + 2 t y = 2 − t y = 2 − t

Question Video Determining the Parametric Equations of a Straight Line

Now recall that in the parametric form of the line the numbers multiplied by \(t\) are the components of the vector that is parallel to the line. Therefore, the vector, \[\vec v = \left\langle {3,12, - 1} \right\rangle \] is parallel to the given line and so must also be parallel to the new line. The equation of new line is then,

Question Video Finding the Parametric Equation of a Line Passing

Lesson 1: Vectors Vector intro for linear algebra Real coordinate spaces Adding vectors algebraically & graphically Multiplying a vector by a scalar Vector examples Scalar multiplication Unit vectors intro Unit vectors Add vectors Add vectors: magnitude & direction to component Parametric representations of lines Math > Linear algebra >

Equation of Complex Straight Line in Parametric form lecture 27

Parametric equations of a straight line refer to expressing the given equation of a line using some arbitrary scalar parameter. For example, y = 2x + 5 y = 2 x + 5 be a line. Let's express it into parametric form. Assign, x = t x = t, we obtain, => y = 2t + 5 => y = 2 t + 5 This is the required set of parametric equations for the given line.

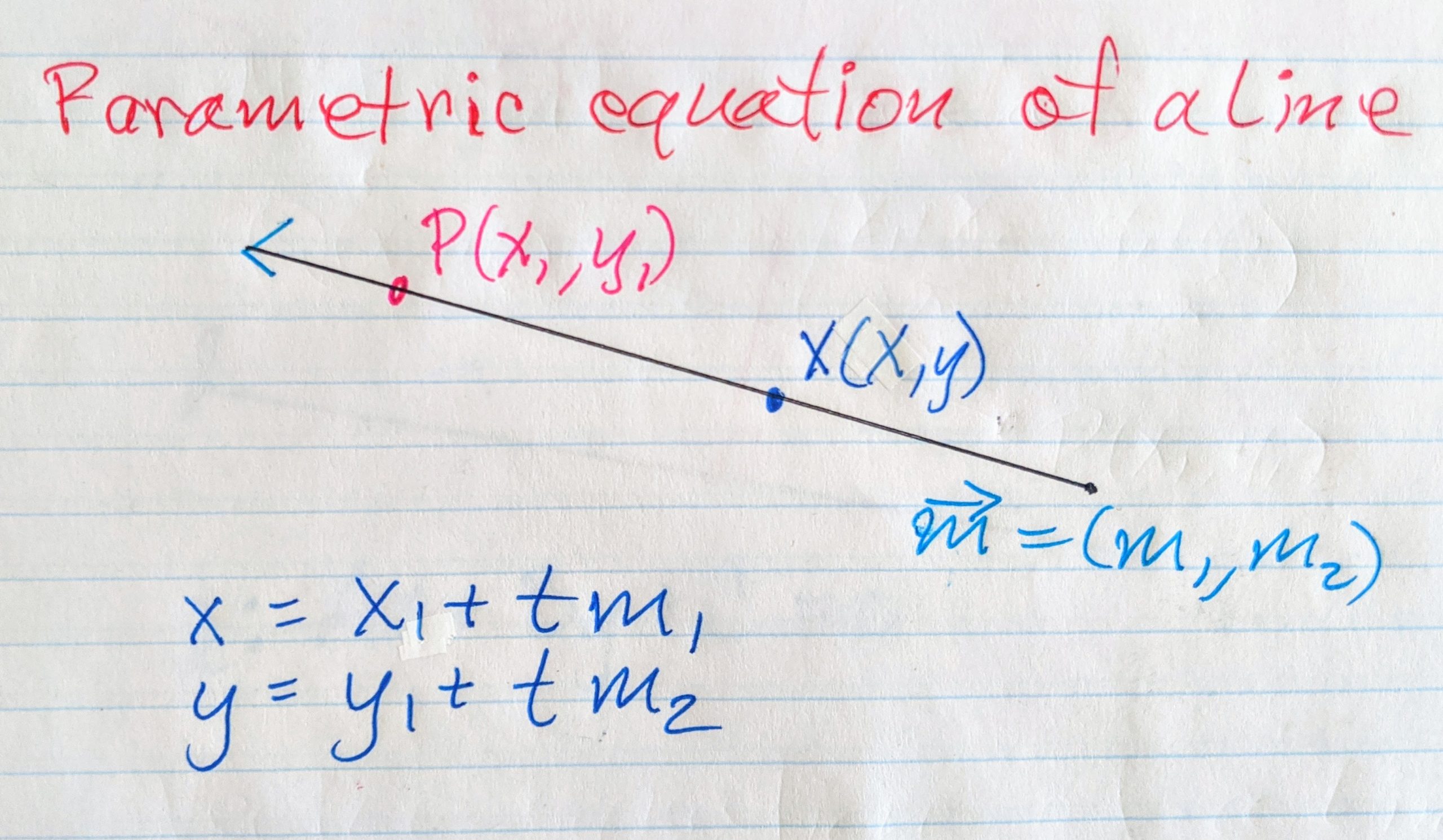
Parametric equation of a line Ottawa, Ontario, Canada Raise My Marks

When parametrizing linear equations, we can begin by letting x = f ( t) and rewrite y wit h this parametrization: y = g ( t). Remember that the standard form of a linear equation is y = m x + b, so if we parametrize x to be equal to t, we'll have the following resulting parametric forms: x = f ( t) y = g ( t) x = t y = m t + b

How To Find The Vector Equation of a Line and Symmetric & Parametric

Equations such as . are called parametric equations, and is called a parameter.. When given an equation of the form , we recognize it as an equation whose graph is a line and we don't need to make a table of values to sketch the graph of the equation.We should be able to do the same for parametric equations of lines. In the next Exploration we will examine our equations carefully to see if.

Question Video Finding Parametric Equations of Straight Lines Nagwa

−1 y(−1) =(−1)2 − 1 = 0 0 0 y(0) =(0)2 − 1 = −1 1 1 y(1) =(1)2 − 1 = 0 2 2 y(2) =(2)2 − 1 = 3 3 3 y(3) =(3)2 − 1 = 8 4 4 y(4) =(4)2 − 1 = 15 t y(t) = t2 − 1 y = x2 − 1 x(t) = t

Parametric equation of a line segment YouTube

d = ‖− − ⇀ aPM × ⇀ v‖ ‖ ⇀ v‖. Example 11.5.3: Calculating the Distance from a Point to a Line. Find the distance between the point M = (1, 1, 3) and line x − 3 4 = y + 1 2 = z − 3. Solution: From the symmetric equations of the line, we know that vector ⇀ v = 4, 2, 1 is a direction vector for the line.

Symmetric Equations of a Line in 3D & Parametric Equations YouTube

About Transcript In this video, we learn about parametric equations using the example of a car driving off a cliff. Parametric equations define x and y as functions of a third parameter, t (time). They help us find the path, direction, and position of an object at any given time. Created by Sal Khan. Questions Tips & Thanks

Parametric Equations of Line Passing Through a Point YouTube

This is known as a parametric equation for the curve that is traced out by varying the values of the parameter t. t. Show that the parametric equation x=\cos t x = cost and y=\sin t y = sint (0 \leqslant t\leqslant 2\pi) (0 ⩽ t⩽ 2π) traces out a circle. Eliminating t t gives x^2+y^2= \cos^2 t+\sin^2 t=1, x2 +y2 = cos2 t+sin2 t = 1,